Quelle est la hauteur de la table? La question posée dans une école en Chine a également mis les meilleurs en difficulté
Les utilisateurs des réseaux sociaux à travers le monde ont résolu obstinément une question qui, selon certaines sources, aurait été proposée aux élèves d’une école primaire en Chine. Malgré l’apparente simplicité, la plupart des personnes qui ont essayé de trouver une solution n’ont pas réussi.
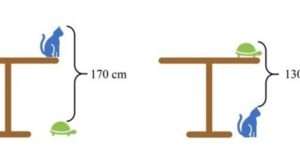
Le texte se lit comme suit: « Trouve la hauteur de la table, sachant que la distance entre la tête du chat sur la table et la tortue sur le sol est de 170 cm, tandis que la distance entre la tête de la tortue sur la table et la tête du chat sur le sol c’est 130 cm « .
Quelle est la hauteur de la table?
solution
Après la diffusion du quiz, les experts ont tenté de donner une solution unique au test, en tenant compte des milliers d’hypothèses issues des tentatives des utilisateurs!
Vous pouvez procéder avec deux types de raisonnement: un algébrique et un visuel.
Méthode algébrique:
En regardant la première figure à gauche, nous pouvons extrapoler cette équation: h. chat + h. table – h. tortue = 170. (h signifie hauteur)
De même, à partir du deuxième chiffre: h. tortue + h. table – h. chat = 130.
En algèbre, on peut additionner deux équations: depuis h. chat et h. Les tortues ont des signes opposés dans les deux équations, s’annulent. L’équation résultante sera: 2 (h h table) = 300, à partir duquel on atteint h. table = 150.
Méthode visuelle:
La deuxième façon de résoudre la question est de penser visuellement: imaginez que vous puissiez superposer les deux images, en faisant coïncider la base du premier tableau (celle de gauche) avec la surface de la seconde (autrement dit, en plaçant l’image à gauche au-dessus du tableau). droit). A partir de cette disposition, nous pouvons comprendre visuellement que la somme des hauteurs 130 cm et 170 cm correspond exactement à la hauteur des deux tables qui se chevauchent, ou 300 cm. Vous pouvez maintenant facilement obtenir la hauteur d’une seule table en divisant la valeur par deux.
Avez-vous pensé que c’était une question impossible?

















